A program megírásához a Gnädig Péter-Honyek Gyula szerzőpáros által kitalált, titánfaló kicsi zöld emberkékről szóló fizika feladatok és az Arrokoth kisbolygó formája adta az ötletet.
Források:
Gnädig Péter-Honyek Gyula: 123 furfangos fizika feladat (1997)
Gnädig Péter-Honyek Gyula-Vigh Máté: 123 furfangos fizika feladat (2014)
KÖMAL P. 4735. feladat (2015/4. szám)
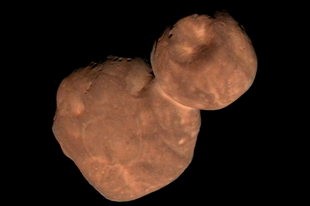
486958 Arrokoth (https://hu.wikipedia.org/wiki/486958_Arrokoth)
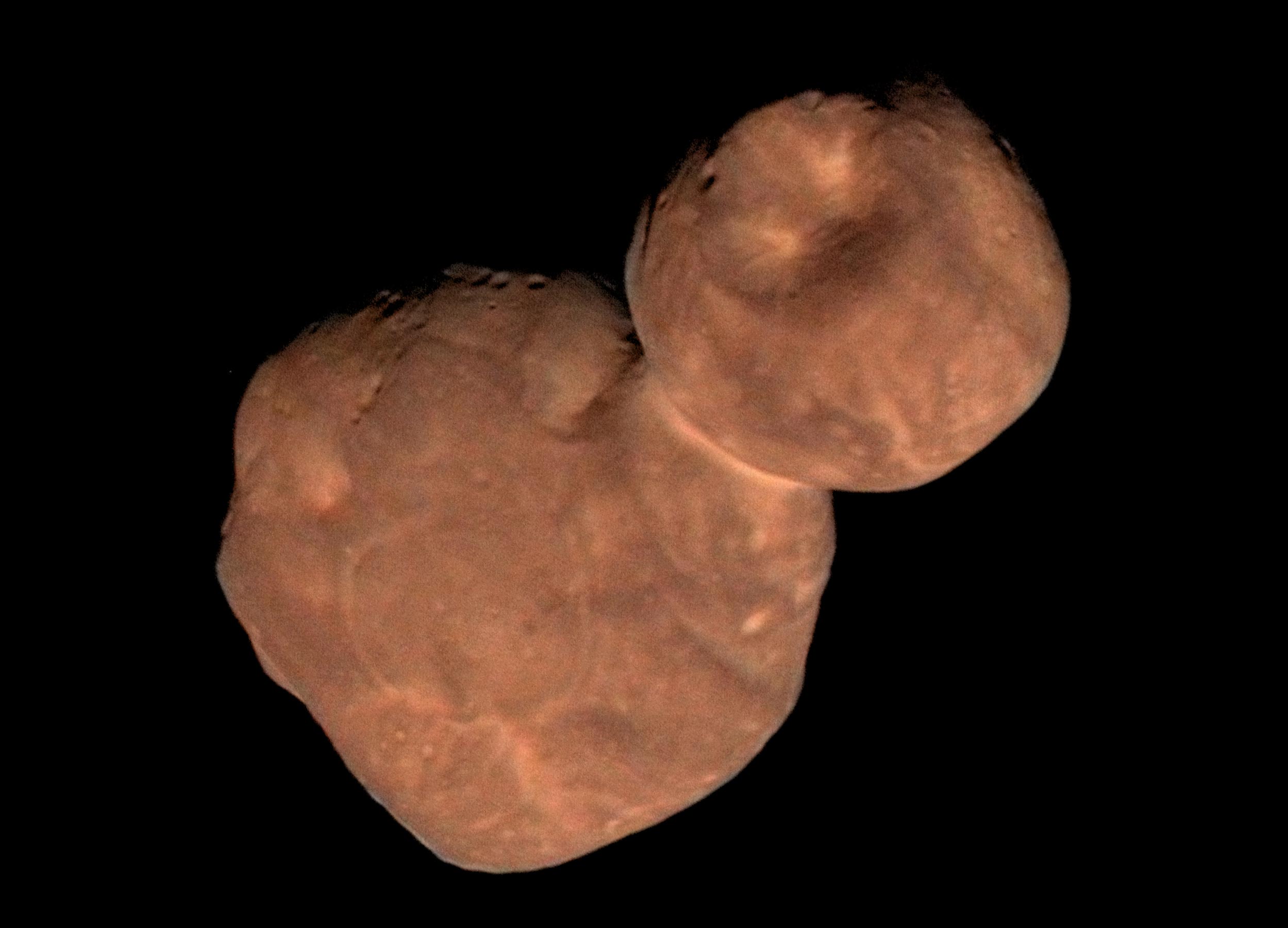
A program célja két homogén tömegeloszlású gömb gravitációs terének szemléltetése. A két gömb kívülről érinti egymást (akár csak az Arrokothnál), vagy az egyik a másikon belül helyezkedik el. Utóbbi esetben gömb alakú üreg is lehetséges (lásd a titánfalók egyik tevékenységét). A program segítségével kétdimenziós színtérkép metszetben, illetve 3D-s megjelenítéssel szemléltethető a gravitációs térerősség (gyorsulás) és potenciál, valamint egy a szimmetria forgástengelyt tartalmazó síkmetszetben ábrázolhatók a gravitációs erővonalak.
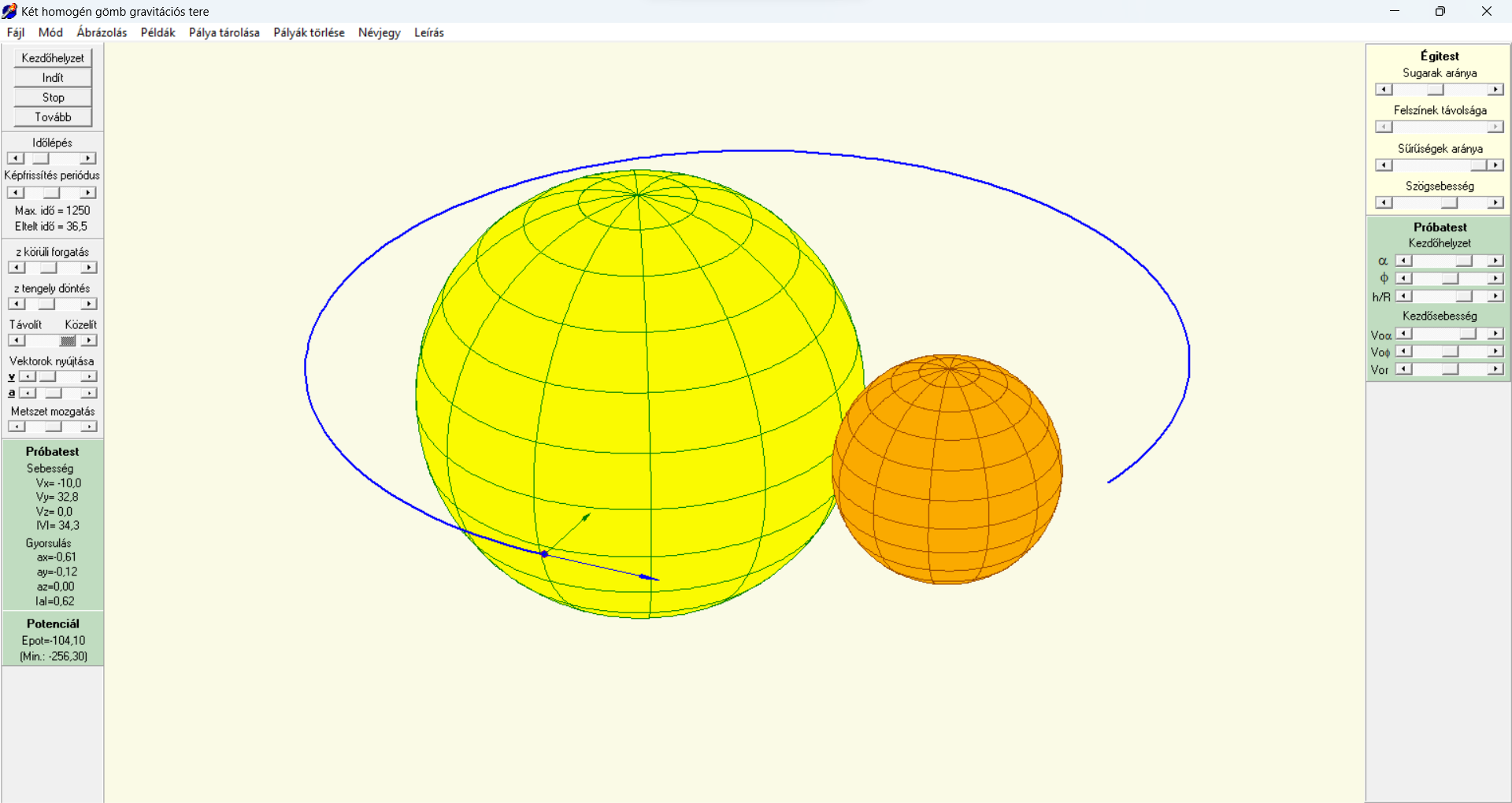
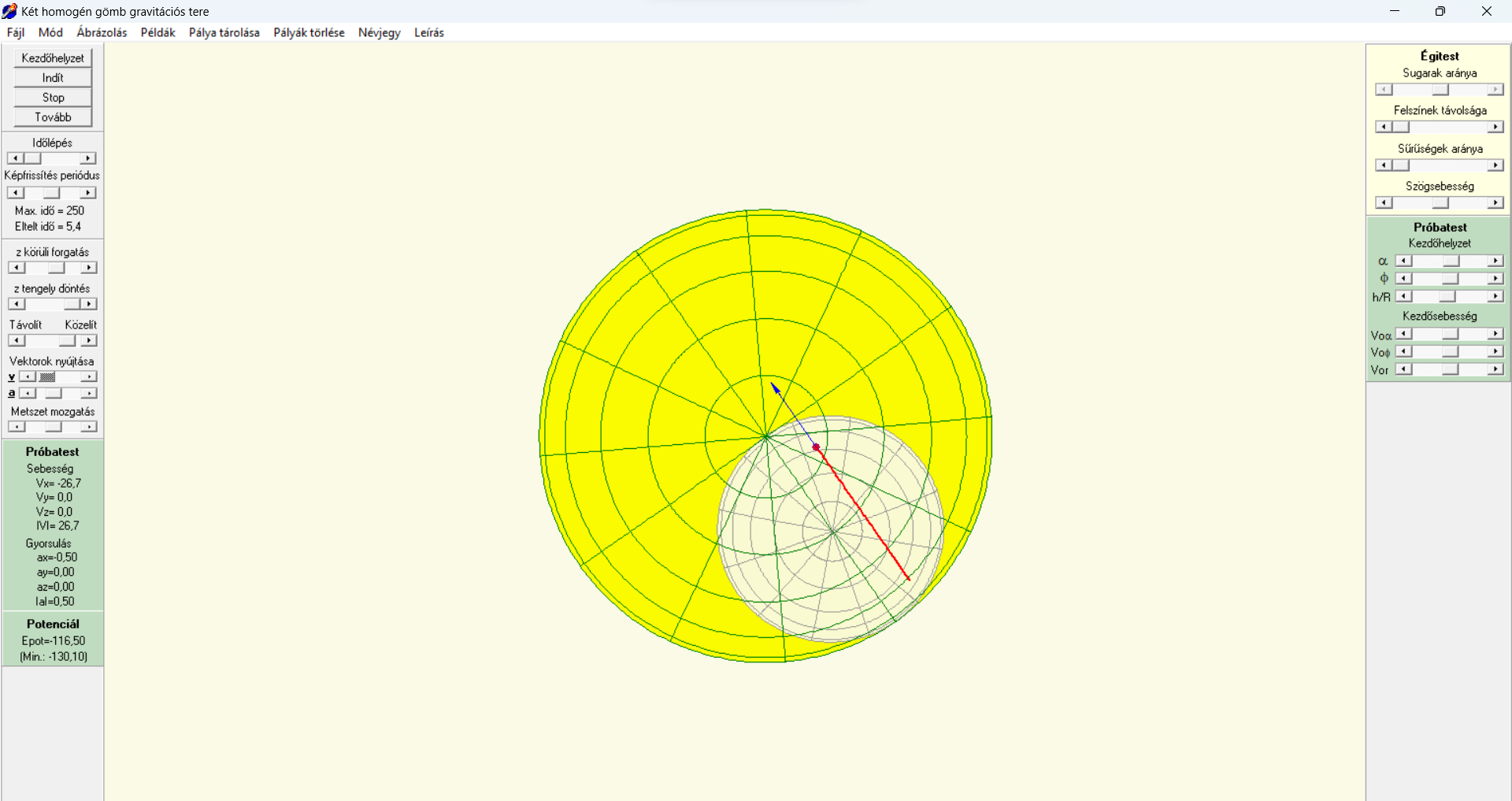
Nyomon követhetjük egy próbatest mozgásának pályáját, sebesség- és gyorsulásvektorát a nyugalomban lévőnek képzelt tömegközépponti, azaz forgás nélküli inerciarendszerből nézve. A szimuláció nyugvó és forgó égitest esetén is lehetséges, de a súrlódást és a közegellenállást elhanyagoljuk. A mozgás létrejöhet a szilárdnak tekintett gömbökön kívül, a nagyobb gömb súrlódásmentes felszínén, egyenes vonalú kényszerpályán/alagútban (ekkor a rendszer nem foroghat, a kényszerpálya kezdő- és végpontja a gömbökben, illetve azok felszínén lehet), vagy a próbatest számára teljesen áthatolhatónak képzelt gömbök esetén is. A számítások során a program negyedrendű Runge-Kutta módszert alkalmaz.
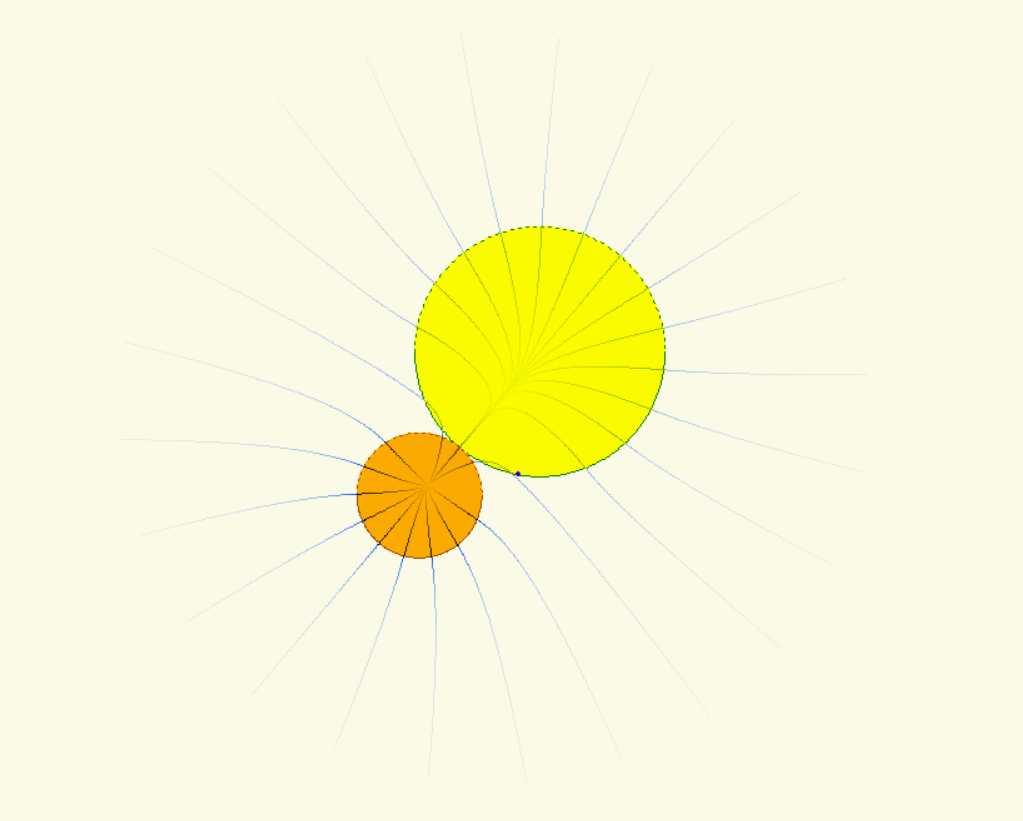

Változtatható paraméterek: a gömbök sugarának aránya, belső gömb esetén a felszínek távolsága, a gömbök sűrűségének aránya, az égitest forgásának szögsebessége, a próbatest kezdőhelyzete és kezdősebessége, a kényszerpálya kezdő- és végpontja, valamint a mozgások szimulációjánál alkalmazott időlépés.
A tömörített program a következő linkről tölthető le: